If you've been trying to write some games on a modern system (ie. your PC), you probably already know about using floats to implement momentum and jumping physics in a 2D platformer, or have something move towards a direction specified in degrees rather than X,Y velocity values to have said object move at an angle, like a ship in an Asteroids style game or a car in a top-down racer... On the PlayStation, these principles still apply. But there's a problem; the PlayStation does not have a hardware floating point unit.
Whilst you can still use floats on the PlayStation as the compiler will resort to software emulation to perform such operations, which you might be able to get away with, it's not exactly the most ideal method as software emulation of floats is quite slow, and will become an issue if used for collision detection or processing movement of a hundred projectile entities... The alternative that's better suited for a system without a floating point unit is to use a integer based fractional number system commonly known as fixed point math.
As the name suggests, fixed point math is a trick for storing fractional numbers with fixed points, in this case an integer scale of 4096 will have a range between zero to 4095 representing a fractional value, with 4096 representing a integer value of 1. Fixed point math is used heavily in games made for systems that lacked a floating point unit (5th generation and older consoles), or where integer math is considerably faster than floating point math and not all systems feature a floating point unit (ie. IBM compatible PCs).
This chapter covers the general idea and basics of performing fixed point integer arithmetic. This is a highly essential chapter when getting into PlayStation homebrew development, as learning it will increase the range of games you can write for the console immensely. If you've already learned some binary encoding of numeric values this chapter might be a bit easier to understand.
Compatible with PSn00bSDK: Yes
The basic principle of fixed point integer math is instead of representing a real number of 1.25 as a floating point number, you instead represent the number as an integer value from a scale value, in this case 4096 which is defined as ONE in the GTE library headers. So a real value of 1.25 will look like 5120 when converted to fixed point math with a scale of 4096. Converting a floating point number to a fixed point number is achieved by simply multiplying the real number against the scale value and rounding off the fractions, turning the result into a plain integer value. The following table shows some sample floating point values represented in fixed point.
| Floating point representation | Fixed point representation |
|---|---|
| 1.25 | 5120 |
| 0.75 | 3072 |
| 0.2 | 819 |
| 21.284 | 87179 |
Using a scale value of 4096 is most ideal for PlayStation projects not only because it provides a good balance between precision and the maximum decimal value it can store, alongside allowing fixed point values to be rounded and divided quickly with simple bit shift operations and AND masks, but also because the Geometry Transformation Engine (GTE) also uses the same scale value for some of its registers. Any scale value can be used to gain more precision or to increase the decimal range limit. Generally a power of two scale value is recommended for performance reasons.
| Bits | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Description | Sign | Decimal (19 bits) | Fractional (12 bits) | |||||||||||||||||||||||||||||
The table above illustrates a fixed point value with a scale value of 4096 in a signed 32-bit integer. As there's only 19 bits available for the decimal portion the maximum range for the decimal value is -524288 to 524287.
Simple mathematical operations in fixed point such as addition and subtraction is not that much different to performing the same operations with integers, only values have to be based around the scale value.
fixed_value += 4096; // += 1.0 fixed_value -= 4096; // -= 1.0 fixed_value += 2048; // += 0.5 fixed_value -= 6144; // -= 1.5
For decimal multiplication and divide operations, the value for the dividend or multiplicand stays as-is.
fixed_value *= 5; // *= 5; fixed_value /= 10; // /= 10;
The equation for performing fractional multiplications is a little tricky, but still not too complicated.
multiplicand = 2048; // multiplicand = 0.5; fixed_value = (fixed_value*multiplicand)>>12; // fixed_value *= multiplicand; multiplicand = 6144; // multiplicand = 1.5; fixed_value = (fixed_value*multiplicand)>>12; // fixed_value *= multiplicand;
For fractional divisions, the value will need to be multiplied by the scale value and then divided by the dividend. Keep in mind that division by zero would still occur if the dividend is zero.
dividend = 2048; // dividend = 0.5; fixed_value = (fixed_value*4096)/dividend; // fixed_value /= dividend; dividend = 6144; // dividend = 1.5; fixed_value = (fixed_value*4096)/dividend; // fixed_value /= dividend;
As a little exercise, this part of the chapter will go through using fixed point math to implement tank controls. The basic jist of this is that instead of moving the player position directly by which direction of the D-pad is pressed, instead, left and right will adjust the angle the player is facing while up and down moves the player forward and backward perpendicular to where the player is facing. To do this requires using sine and cosine values and conveniently, the GTE libraries of both SDKs feature integer based sine and cosine functions which is exactly what's needed for this exercise.
In the official PsyQ or Programmer's Tool SDKs there are two integer based sine and cosine functions which are rsin()/rcos() and csin()/ccos(). The differences between the two is that rsin()/rcos() takes up less code but is slower, whereas csin()/ccos() takes up more code but is faster. PSn00bSDK on the other hand only has one set of functions called isin()/icos(), which are based on a Taylor series implementation which is both small and fast. PSn00bSDK provides definitions for rsin()/rcos() and csin()/ccos() that simply points to isin()/icos() for compatibility with PsyQ / Programmer's Tool projects and sample code.
These functions also take degrees in a fixed point range of 0 to 4096 where 4096 equals to 360 degrees, so a value of 45 degrees will be specified as 512. The value returned is also in a fixed point notation with a scale of 4096, where 4096 equals to 1.0.
Working from code from the controllers chapter, rewrite the code that defines the initial values of the player position to begin at the center of the screen. Because the player coordinates will be in fixed point, the screen center coordinate must be multiplied by ONE.
pos_x = ONE*(disp[0].disp.w>>1); pos_y = ONE*(disp[0].disp.h>>1);
Then, define a new variable for the player's angle and set the initial value to zero.
int angle; angle = 0;
The player will be represented as a rotating triangle in this chaper, so a simple array of vector coordinates will define the shape of the triangle. The triangle will be rotated with, you guessed it, fixed point math as well.
SVECTOR player_tri[] =
{
{ 0, -20, 0 },
{ 10, 20, 0 },
{ -10, 20, 0 }
};
Then ditch the code for sorting TILE and SPRT primitives and replace it with the following routine that sorts a rotating triangle.
POLY_F3 *tri;
...
// Rotate the triangle coordinates based on the player's angle
// as well as apply the position
for( i=0; i<3; i++ )
{
v[i].vx = (((player_tri[i].vx*ccos( angle ))
-(player_tri[i].vy*csin( angle )))>>12)+(pos_x>>12);
v[i].vy = (((player_tri[i].vy*ccos( angle ))
+(player_tri[i].vx*csin( angle )))>>12)+(pos_y>>12);
}
// Sort the player triangle
tri = (POLY_F3*)nextpri;
setPolyF3( tri );
setRGB0( tri, 255, 255, 0 );
setXY3( tri,
v[0].vx, v[0].vy,
v[1].vx, v[1].vy,
v[2].vx, v[2].vy );
addPrim( ot[db], tri );
nextpri += sizeof(POLY_F3);
And then replace the input code with the following. If you've written something that played like Asteroids in the past, this may look pretty familiar.
if( !(pad->btn&PAD_UP) ) // test UP
{
pos_x += csin( angle );
pos_y -= ccos( angle );
}
else if( !(pad->btn&PAD_DOWN) ) // test DOWN
{
pos_x -= csin( angle );
pos_y += ccos( angle );
}
if( !(pad->btn&PAD_LEFT) ) // test LEFT
{
// Turns counter-clockwise
angle -= 16;
}
else if( !(pad->btn&PAD_RIGHT) ) // test RIGHT
{
// Turns clockwise
angle += 16;
}
Next is to finally add some text drawing so the player coordinates can be
displayed on screen, so you can see how fixed point numbers work while
interacting with the sample program more easily. This can be done with the
debug font functions provided by
Start by loading the debug font texture to VRAM using FntLoad(), then, initialize a font window using FntOpen(). Ideally, you should put these calls inside the init() function.
// Load the font texture on the upper-right corner of the VRAM FntLoad( 960, 0 ); // Define a font window of 100 characters covering the whole screen FntOpen( 0, 8, 320, 224, 0, 100 );
Text can be printed using FntPrint() which works more or less like printf(), only text output is directed to the specified font window. The first argument specifies which font window the text should go to, the value of which is obtained through the return value of FntOpen(). Specifying -1 directs text to the last opened font window. The debug font routines can only draw uppercase text, and text color and font cannot be customized.
In PsyQ / Programmers tool the first argument can be omitted, but modern GNU GCC does not support this convention anymore.
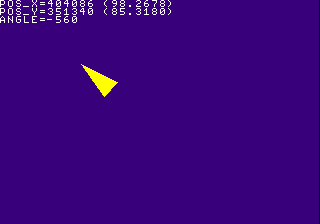
// Print player coordinates FntPrint( -1, "POS_X=%d (%d.%d)\n", pos_x, (pos_x>>12), (pos_x&0xfff) ); FntPrint( -1, "POS_Y=%d (%d.%d)\n", pos_y, (pos_y>>12), (pos_y&0xfff) ); FntPrint( -1, "ANGLE=%d\n", angle );
Then to make the text actually appear, call FntFlush() to draw the characters 'printed' by FntPrint() and flush the character buffer. This should be called immediately before the display() call in the sample code.
// Draw and flush the character buffer FntFlush( -1 );
The finished code should look like the following (the texture stuff remains for future samples):
#include <sys/types.h> // This provides typedefs needed by libgte.h and libgpu.h
#include <stdio.h> // Not necessary but include it anyway
#include <psxetc.h> // Includes some functions that controls the display
#include <psxgte.h> // GTE header, not really used but libgpu.h depends on it
#include <psxgpu.h> // GPU library header
#include <psxapi.h>
#define OTLEN 8 // Ordering table length (recommended to set as a define
// so it can be changed easily)
DISPENV disp[2]; // Display/drawing buffer parameters
DRAWENV draw[2];
int db = 0;
// PSn00bSDK requires having all u_long types replaced with
// u_int, as u_long in modern GCC that PSn00bSDK uses defines it as a 64-bit integer.
u_int ot[2][OTLEN]; // Ordering table length
char pribuff[2][32768]; // Primitive buffer
char *nextpri; // Next primitive pointer
int tim_mode; // TIM image parameters
RECT tim_prect,tim_crect;
int tim_uoffs,tim_voffs;
// Pad stuff
#define PAD_SELECT 1
#define PAD_L3 2
#define PAD_R3 4
#define PAD_START 8
#define PAD_UP 16
#define PAD_RIGHT 32
#define PAD_DOWN 64
#define PAD_LEFT 128
#define PAD_L2 256
#define PAD_R2 512
#define PAD_L1 1024
#define PAD_R1 2048
#define PAD_TRIANGLE 4096
#define PAD_CIRCLE 8192
#define PAD_CROSS 16384
#define PAD_SQUARE 32768
typedef struct _PADTYPE
{
unsigned char stat;
unsigned char len:4;
unsigned char type:4;
unsigned short btn;
unsigned char rs_x,rs_y;
unsigned char ls_x,ls_y;
} PADTYPE;
u_char padbuff[2][34];
// For the player triangle
SVECTOR player_tri[] = {
{ 0, -20, 0 },
{ 10, 20, 0 },
{ -10, 20, 0 }
};
void display() {
DrawSync(0); // Wait for any graphics processing to finish
VSync(0); // Wait for vertical retrace
PutDispEnv(&disp[db]); // Apply the DISPENV/DRAWENVs
PutDrawEnv(&draw[db]);
SetDispMask(1); // Enable the display
DrawOTag(ot[db]+OTLEN-1); // Draw the ordering table
db = !db; // Swap buffers on every pass (alternates between 1 and 0)
nextpri = pribuff[db]; // Reset next primitive pointer
}
// Texture upload function
void LoadTexture(u_int *tim, TIM_IMAGE *tparam) {
// Read TIM parameters (PsyQ)
//OpenTIM(tim);
//ReadTIM(tparam);
// Read TIM parameters (PSn00bSDK)
GetTimInfo(tim, tparam);
// Upload pixel data to framebuffer
LoadImage(tparam->prect, tparam->paddr);
DrawSync(0);
// Upload CLUT to framebuffer if present
if( tparam->mode & 0x8 ) {
LoadImage(tparam->crect, tparam->caddr);
DrawSync(0);
}
}
void loadstuff(void) {
TIM_IMAGE my_image; // TIM image parameters
extern u_int tim_my_image[];
// Load the texture
LoadTexture(tim_my_image, &my_image);
// Copy the TIM coordinates
tim_prect = *my_image.prect;
tim_crect = *my_image.crect;
tim_mode = my_image.mode;
// Calculate U,V offset for TIMs that are not page aligned
tim_uoffs = (tim_prect.x%64)<<(2-(tim_mode&0x3));
tim_voffs = (tim_prect.y&0xff);
}
// To make main look tidy, init stuff has to be moved here
void init(void) {
// Reset graphics
ResetGraph(0);
// First buffer
SetDefDispEnv(&disp[0], 0, 0, 320, 240);
SetDefDrawEnv(&draw[0], 0, 240, 320, 240);
// Second buffer
SetDefDispEnv(&disp[1], 0, 240, 320, 240);
SetDefDrawEnv(&draw[1], 0, 0, 320, 240);
draw[0].isbg = 1; // Enable clear
setRGB0(&draw[0], 63, 0, 127); // Set clear color (dark purple)
draw[1].isbg = 1;
setRGB0(&draw[1], 63, 0, 127);
nextpri = pribuff[0]; // Set initial primitive pointer address
// load textures and possibly other stuff
loadstuff();
// set tpage of lone texture as initial tpage
draw[0].tpage = getTPage( tim_mode&0x3, 0, tim_prect.x, tim_prect.y );
draw[1].tpage = getTPage( tim_mode&0x3, 0, tim_prect.x, tim_prect.y );
// apply initial drawing environment
PutDrawEnv(&draw[!db]);
// Initialize the pads
InitPAD( padbuff[0], 34, padbuff[1], 34 );
// Begin polling
StartPAD();
// To avoid VSync Timeout error, may not be defined in PsyQ
ChangeClearPAD( 1 );
// Load the font texture on the upper-right corner of the VRAM
FntLoad( 960, 0 );
// Define a font window of 100 characters covering the whole screen
FntOpen( 0, 8, 320, 224, 0, 100 );
}
int main() {
int i;
int pos_x,pos_y,angle;
PADTYPE *pad;
POLY_F3 *tri;
SVECTOR v[3];
TILE *tile; // Pointer for TILE
SPRT *sprt; // Pointer for SPRT
// Init stuff
init();
pos_x = ONE*(disp[0].disp.w>>1);
pos_y = ONE*(disp[0].disp.h>>1);
angle = 0;
while(1) {
// Parse controller input
pad = (PADTYPE*)padbuff[0];
// Only parse inputs when a controller is connected
if( pad->stat == 0 )
{
// Only parse when a digital pad,
// dual-analog and dual-shock is connected
if( ( pad->type == 0x4 ) ||
( pad->type == 0x5 ) ||
( pad->type == 0x7 ) )
{
if( !(pad->btn&PAD_UP) ) // test UP
{
pos_x += csin( angle );
pos_y -= ccos( angle );
}
else if( !(pad->btn&PAD_DOWN) ) // test DOWN
{
pos_x -= csin( angle );
pos_y += ccos( angle );
}
if( !(pad->btn&PAD_LEFT) ) // test LEFT
{
angle -= 16;
}
else if( !(pad->btn&PAD_RIGHT) ) // test RIGHT
{
angle += 16;
}
}
}
ClearOTagR(ot[db], OTLEN); // Clear ordering table
// Rotate the triangle coordinates based on the player's angle
// as well as apply the position
for( i=0; i<3; i++ )
{
v[i].vx = (((player_tri[i].vx*icos( angle ))
-(player_tri[i].vy*csin( angle )))>>12)+(pos_x>>12);
v[i].vy = (((player_tri[i].vy*icos( angle ))
+(player_tri[i].vx*csin( angle )))>>12)+(pos_y>>12);
}
// Sort the player triangle
tri = (POLY_F3*)nextpri;
setPolyF3( tri );
setRGB0( tri, 255, 255, 0 );
setXY3( tri,
v[0].vx, v[0].vy,
v[1].vx, v[1].vy,
v[2].vx, v[2].vy );
addPrim( ot[db], tri );
nextpri += sizeof(POLY_F3);
// Print player coordinates
FntPrint( -1, "POS_X=%d (%d.%d)\n", pos_x, (pos_x>>12), (pos_x&0xfff) );
FntPrint( -1, "POS_Y=%d (%d.%d)\n", pos_y, (pos_y>>12), (pos_y&0xfff) );
FntPrint( -1, "ANGLE=%d\n", angle );
// Draw and flush the character buffer
FntFlush( -1 );
// Update the display
display();
}
return 0;
}
Compile and execute the code and you should get a triangle that controls more or less like a tank. Press the left and right directional buttons to turn the triangle while pressing up and down moves the triangle forwards and backward perpendicular to where the triangle is pointing.

Now to make the tank controls sample a little more interesting by making it control like an Asteroids or Spacewar game. Basically, instead of accumulating the player coordinates directly with values based on the player's angle you accumulate them to a velocity vector, which in turn accumulates on the player's coordinates. This way, simple momentum based physics are archieved.
This can be done by implementing some changes to the last sample. Start by adding variables in main() that'll be used to store the player's velocity coordinates.
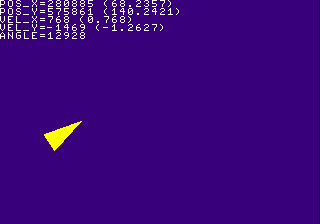
int vel_x,vel_y; ... // just to make sure they don't contain garbage vel_x = 0; vel_y = 0;
Next, modify some of the pad code to accumulate player movement towards the velocity variables instead of the player's coordinates. Put some bit shifts that divides the sin/cos values by 8 otherwise the 'ship' will accelerate too quickly.
if( !(pad->btn&PAD_UP) ) // test UP
{
vel_x += csin( angle )>>3;
vel_y -= ccos( angle )>>3;
}
else if( !(pad->btn&PAD_DOWN) ) // test DOWN
{
vel_x -= csin( angle )>>3;
vel_y += ccos( angle )>>3;
}
Immediately after the pad code add a few lines that accumulates the velocity coordinates to the player's coordinates.
// accumulate player coordinates by its velocity pos_x += vel_x; pos_y += vel_y;
And to keep the player from going off-screen, place the following lines immediately after the above code to wrap the player's coordinates when they go off-screen.
// wrap player coordinates from going off-screen
if( (pos_x>>12) < 0 )
{
pos_x += (320<<12);
}
if( (pos_x>>12) > 320 )
{
pos_x -= (320<<12);
}
if( (pos_y>>12) < 0 )
{
pos_y += (240<<12);
}
if( (pos_y>>12) > 240 )
{
pos_y -= (240<<12);
}
Then place some additional FntPrint() calls that displays the values from the velocity variables. You'll also need to increase the character buffer size of the FntOpen() call (the last argument) from 100 to 150.
FntPrint( -1, "VEL_X=%d (%d.%d)\n", vel_x, (vel_x>>12), (vel_x&0xfff) ); FntPrint( -1, "VEL_Y=%d (%d.%d)\n", vel_y, (vel_y>>12), (vel_y&0xfff) );
Compile the sample demo and the triangle should behave a lot like an Asteroids ship.
If you want velocity to slowly diminish overtime, add the following lines just before the velocity vectors are accumulated to the player coordinates. It also acts as a velocity constraint as well.
// equivalent to multiplying each axis by 0.9765625 vel_x = (vel_x*4000)>>12; vel_y = (vel_y*4000)>>12;
Since it is something new programmers would find incredibly handy and to show off some of what the 32-bit console can do, especially for PSn00bSDK folk as it does not have an equivalent to libgs, here's a fixed point based sprite rotation and scaling routine that draws a rotated and scaled sprite with a single quad. The math for rotation is more or less the same as how the player triangle is rotated.
void sortRotSprite( int x, int y, int pw, int ph, int angle, int scale )
{
POLY_FT4 *quad;
SVECTOR s[4];
SVECTOR v[4];
int i,cx,cy;
// calculate the pivot point (center) of the sprite
cx = pw>>1;
cy = ph>>1;
// increment by 0.5 on the bottom and right coords so scaling
// would increment a bit smoother
s[0].vx = -(((pw*scale)>>12)-cx);
s[0].vy = -(((ph*scale)>>12)-cy);
s[1].vx = (((pw*scale)+2048)>>12)-cx;
s[1].vy = s[0].vy;
s[2].vx = -(((pw*scale)>>12)-cx);
s[2].vy = (((ph*scale)+2048)>>12)-cy;
s[3].vx = (((pw*scale)+2048)>>12)-cx;
s[3].vy = s[2].vy;
// a simple but pretty effective optimization trick
cx = ccos( angle );
cy = csin( angle );
// calculate rotated sprite coordinates
for( i=0; i<4; i++ )
{
v[i].vx = (((s[i].vx*cx)
-(s[i].vy*cy))>>12)+x;
v[i].vy = (((s[i].vy*cx)
+(s[i].vx*cy))>>12)+y;
}
// initialize the quad primitive for the sprite
quad = (POLY_FT4*)nextpri;
setPolyFT4( quad );
// set CLUT and tpage to the primitive
setTPage( quad, tim_mode&0x3, 0, tim_prect.x, tim_prect.y );
setClut( quad, tim_crect.x, tim_crect.y );
// set color, screen coordinates and texture coordinates of primitive
setRGB0( quad, 128, 128, 128 );
setXY4( quad,
v[0].vx, v[0].vy,
v[1].vx, v[1].vy,
v[2].vx, v[2].vy,
v[3].vx, v[3].vy );
setUVWH( quad, tim_uoffs, tim_voffs, pw, ph );
// add it to the ordering table
addPrim( ot[db], quad );
nextpri += sizeof(POLY_FT4);
}
By this point, it should be easy to figure out how to use this function in the sample above. The angle and scale arguments are of a fixed point notation, where 4096 is 360 degrees on the former and 4096 is 1.0 on the latter.
One limitation that becomes apparent when performing 32-bit fixed point math arithmetic is when performing fractional multiplication operations with large fixed point values due to the C compiler usually always performing multiplication and bit shifting operations with 32-bit registers, as multiplying a large fixed point value by a large fixed point multiplicand will likely exceed the capacity of a 32-bit word, yielding a faulty result.
The MIPS R3000 CPU of the PlayStation can actually return a 64-bit multiplication result, but the C compiler doesn't really make use of this trait when performing multiplication operations with 32-bit integers. So the only way to effectively take advantage of this is to use some in-line assembly code. Should be pretty self explanatory on how and where it should be used.
/* in-line assembly macro for performing multiplication */
/* operations with 12-bit fractions. Uses what is effectively */
/* 64-bit maths with both hi and lo result registers to avoid */
/* overflow bugs when using 32-bit maths. */
/* */
/* Performs r2 = ( r0 * r1 )>>12 with 64-bit arithmetic */
/* */
#define mult12( r0, r1, r2 ) __asm__ volatile ( \
"mult %1, %0;" /* multiply values (small * large is faster) */\
"mflo $t0;" /* retrieve the 64-bit result in two regs */\
"mfhi $t1;" \
"srl $t0, 12;" /* equivalent to dividing LO by 4096 */\
"and $t1, 0x0fff;" /* mask HI result to fit in upper 12 bits of */\
"sll $t1, 20;" /* LO result, then shift bits to position */\
"or $t0, $t1;" /* combine the bits */\
"sw $t0, ( %2 );" /* store the result to r2 */\
: \
: "r"( r0 ), "r"( r1 ), "r"( r2 ) \
: "lo", "hi", "t0", "t1", "memory" )
Though naturally, fixed point math can't really be as precise as floating point math in certain operations. You can try increasing precision by increasing the base value, alloting more bits for the fractional part of a fixed point value, but there will still be something rough about it.
This chapter only really covers some pretty basic but highly essential math operations with fixed point math, but it should be enough to get you started in learning the practice. Interestingly fixed point math is still somewhat talked about around the modern Internet, so you may want to look around for those for further reading if need-be.
| Previous | Back to Index | Next |